40. Паралельне з’єднання провідників

Назад до змісту

КОНТРОЛЬНІ ЗАПИТАННЯ

1. Назвіть характерну ознаку кола, яке містить паралельне з’єднання провідників.

Ознака паралельного кола — є розгалуження, де струм іде двома або більше шляхами (вітками), які під’єднані до спільних двох вузлів.

2. Порівняйте напругу на ділянці кола, яка складається з паралельно з’єднаних провідників, і напруги на кожному провіднику.

Напруга на всій паралельній ділянці така сама, як і на кожному провіднику в цій ділянці.

3. Яким є співвідношення між силою струму в нерозгалуженій частині кола і силою струму в кожній вітці розгалуження?

Струм у нерозгалуженій частині дорівнює сумі струмів у всіх вітках.

4. За допомогою якої формули можна обчислити опір ділянки кола, яка складається з кількох паралельно з’єднаних провідників?

Загальний опір для nn паралельно з’єднаних провідників знаходять так:

\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dots+\dfrac{1}{R_n}

5. Чому споживачі електроенергії у вашій оселі з’єднано паралельно?

Паралельне з’єднання використовується для того, щоб на кожному приладі була однакова напруга (стандартна мережева 220 В), на яку вони розраховані. Крім того, це дозволяє вмикати та вимикати кожен прилад незалежно від інших.

ВПРАВА № 40

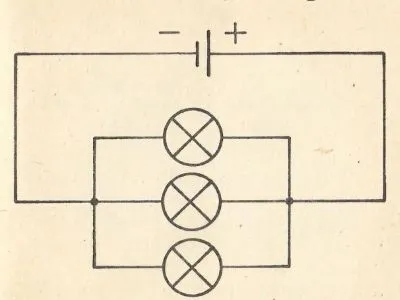
1. Електричне коло складається з акумулятора та трьох з’єднаних паралельно електричних ламп. Накресліть електричну схему цього кола.

Електричне коло складається з акумулятора та трьох з’єднаних паралельно електричних ламп

2. На рис. 1 зображено схему ділянки електричного кола. Відомо, що опір R1 становить 100 Ом, опір R2 — 150 Ом, показ амперметра — 2,4 А. Визначте напругу на ділянці

На рис. 1 зображено схему ділянки електричного кола

Дано:

R_1=100 \,\text{Ом}

R_2=150 \,\text{Ом}

I=2{,}4 \,\text{А}

Знайти:

U-?

Розв’язання:

Оскільки з’єднання паралельне, еквівалентний опір:

R=\dfrac{R_1 \cdot R_2}{R_1+R_2}=\dfrac{100 \cdot 150}{100+150}=\dfrac{15000}{250}=60 \,\text{Ом}

Тоді напруга на ділянці:

U=I \cdot R=2{,}4 \cdot 60=144 \,\text{В}

Відповідь: Напруга на ділянці кола становить 144 В.

3. Дві електричні лампи з’єднали паралельно й приєднали до джерела струму, напруга на виході якого становить 120 В. Визначте силу струму в кожній лампі й у нерозгалуженій частині кола, якщо опір однієї лампи дорівнює 200 Ом, а іншої — 300 Ом.

Дано:

U=120 \,\text{В}

R_1=200 \,\text{Ом}

R_2=300 \,\text{Ом}

Знайти:

I_1-?

I_2-?

I-?

Розв’язання:

При паралельному з’єднанні:

U_1=U_2=U=120 \,\text{В}

Струм у кожній лампі:

I_1=\dfrac{U}{R_1}=\dfrac{120}{200}=0{,}6 \,\text{ А}

I_2=\dfrac{U}{R_2}=\dfrac{120}{300}=0{,}4 \,\text{ А}

Струм у нерозгалуженій частині:

I=I_1+I_2=0{,}6+0{,}4=1{,}0 \,\text{А}

Відповідь: Сила струму в першій лампі — 0,6 А, у другій — 0,4 А, у нерозгалуженій частині кола — 1 А.

4. Однакові за довжиною та поперечним перерізом дроти — залізний, мідний і срібний — з’єднали паралельно та підключили до джерела струму. У якому дроті сила струму буде найбільшою?

Найбільший струм буде у срібному дроті. За паралельного з’єднання напруга однакова, тому з формули

I=\dfrac{U}{R}

видно: менший опір — більший струм. Оскільки розміри дротів однакові, то

R=\rho \dfrac{l}{S}

і все вирішує питомий опір ρ: у срібла він найменший, отже струм — найбільший.

5. Визначте загальний опір ділянки кола, зображеної на рис. 40.5, б, якщо R1=R6=7 Ом; R2=1 Ом; R3=5 Ом; R4=12 Ом; R5=4 Ом. Якою буде загальна сила струму в ділянці кола, якщо до неї прикласти напругу 4 В?

Визначте загальний опір ділянки кола, зображеної на рис. 40.5

Дано:

R_1=7 \,\text{Ом}

R_6=7 \,\text{Ом}

R_2=1 \,\text{Ом}

R_3=5 \,\text{Ом}

R_4=12 \,\text{Ом}

R_5=4 \,\text{Ом}

U=4 \,\text{В}

Знайти:

R_{\text{заг}}-?

I_{\text{заг}}-?

Розв’язання:

Паралельно з’єднані R4 і R5:

R_{4,5}=\dfrac{R_4 \cdot R_5}{R_4+R_5}=\dfrac{12 \cdot 4}{12+4}=\dfrac{48}{16}=3 \,\text{Ом}

Ліва гілка (послідовно R1 і R3):

R_{1,3}=R_1+R_3=7+5=12 \,\text{Ом}

Права гілка (послідовно R2 і R4,5):

R_{2,4,5}=R_2+R_{4,5}=1+3=4 \,\text{Ом}

Паралельне з’єднання двох гілок:

R_{\text{пар}}=\dfrac{R_{1,3} \cdot R_{2,4,5}}{R_{1,3}+R_{2,4,5}}=\dfrac{12 \cdot 4}{12+4}=\dfrac{48}{16}=3 \,\text{Ом}

Повний опір (послідовно Rпар і R6):

R_{\text{заг}}=R_{\text{пар}}+R_6=3+7=10 \,\text{Ом}

Загальний струм:

I=\dfrac{U}{R_{\text{заг}}}=\dfrac{4}{10}=0{,}4 \,\text{А}

Відповідь: Загальний опір ділянки кола становить 10 Ом. Загальна сила струму дорівнює 0,4 А.

6. Визначте, чому дорівнює напруга на полюсах джерела струму, яке живить коло (рис. 2), якщо R1 = 3 Ом; R2 = 2 Ом; R3 = 8 Ом. Показ амперметра — 0,1 А.

Визначте, чому дорівнює напруга на полюсах джерела струму, яке живить коло (рис. 2)

Дано:

R_1=3 \,\text{Ом}

R_2=2 \,\text{Ом}

R_3=8 \,\text{Ом}

I_3=0{,}1 \,\text{А}

Знайти:

U-?

Розв’язання:

Оскільки R2 і R3 паралельно, напруга на них однакова:

U_{2,3}=U_3=I_3 \cdot R_3=0{,}1 \cdot 8=0{,}8 \,\text{В}

Струм у вітці з R2:

I_2=\dfrac{U_{2,3}}{R_2}=\dfrac{0{,}8}{2}=0{,}4 \,\text{А}

Загальний струм (через R1):

I=I_2+I_3=0{,}4+0{,}1=0{,}5 \,\text{А}

Напруга на R1:

U_1=I \cdot R_1=0{,}5 \cdot 3=1{,}5 \,\text{В}

Напруга джерела:

U=U_1+U_{2,3}=1{,}5+0{,}8=2{,}3 \,\text{В}

Відповідь: Напруга на полюсах джерела струму дорівнює 2,3 В.

7. Ви маєте 4 резистори з опором R0 кожний. Скільки різних опорів і які саме ви можете отримати, використовуючи всі резистори одночасно?

Можна отримати 9 різних значень:

Послідовно всі 4: $4R_0$
Паралельно всі 4: $\dfrac{1}{4}R_0$
Дві паралельні пари послідовно (або дві послідовні пари паралельно): $R_0$
Три послідовно, ця трійка паралельно четвертому: $\dfrac{3}{4}R_0$
Три паралельно, ця трійка послідовно з четвертим: $\dfrac{4}{3}R_0$
Дві послідовно, ця група паралельно двом іншим, що з’єднані паралельно між собою: $\dfrac{2}{5}R_0$
Дві паралельно, ця група послідовно з двома іншими (послідовними): $\dfrac{5}{2}R_0$
Два послідовно (група $2R_0$ ) паралельно одному ( $R_0$ ), і ця вся ділянка послідовно з четвертим: $\dfrac{5}{3}R_0$
Два паралельно, послідовно з одним (група $\dfrac{3}{2}R_0$ ), і ця вся ділянка паралельно четвертому: $\dfrac{3}{5}R_0$

8. Опір усіх резисторів на ділянці електричного кола (рис. 3) є однаковим і дорівнює 5 Ом. До ділянки кола прикладено незмінну напругу. Який ключ потрібно замкнути, щоб показ амперметра A2 був нижчим від показу амперметра A1? Яке значення сили струму буде показувати амперметр A1, якщо замкнути тільки ключ К1? Відомо, що амперметр A2 показує 300 мА, якщо всі ключі розімкнені.

Опір усіх резисторів на ділянці електричного кола (рис. 3) є однаковим і дорівнює 5 Ом

Дано:

R_1=R_2=R_3=R_4=R=5 \,\text{Ом}

U=\text{незмінна}

I_{A2}=300 \,\text{мА}=0{,}3 \,\text{А} \ \ (\text{усі ключі розімкнені})

Знайти:

I_1-?

Розв’язання:

Коли всі ключі розімкнені, струм іде послідовно через R1 і R2, а гілки з R3 та R4 вимкнені. Амперметри A1 і A2 тоді показують однаковий струм, бо розгалуження немає.

Повний опір:

R_{\text{заг1}}=R_1+R_2=5+5=10 \,\text{Ом}

Напруга джерела:

U=I \cdot R_{\text{заг1}}=0{,}3 \cdot 10=3 \,\text{В}

Щоб $I_{A2} < I_{A1}$ , після R1 має з’явитися обхідна гілка, тоді частина струму піде не через A2. На схемі цей обхід проходить через гілку з R3, тому треба замкнути ключ K2.

Якщо замкнути тільки K1, тоді R2 і R4 з’єднуються паралельно:

R_{2,4}=\dfrac{R \cdot R}{R+R}=\dfrac{5 \cdot 5}{5+5}=2{,}5 \,\text{Ом}

Повний опір:

R_{\text{заг2}}=R_1+R_{2,4}=5+2{,}5=7{,}5 \,\text{Ом}

Струм, який покаже A1:

I=\dfrac{U}{R_{\text{заг2}}}=\dfrac{3}{7{,}5}=0{,}4 \,\text{А}

Відповідь: щоб $I_{A2} < I_{A1}$ , потрібно замкнути ключ K2. Якщо замкнути тільки K1, амперметр A1 покаже 0,4 А (400 мА).

9. Щоб виміряти силу струму, більшу за ту, на яку розрахований амперметр, можна скористатися тим самим амперметром: паралельно амперметру необхідно під’єднати резистор — шунт (рис. 4). У разі застосування шунта струм ділиться на дві частини: одна йде через амперметр, а друга — через шунт: I = IА +1ш . Шунт якого опору треба під’єднати паралельно амперметру опором 0,07 Ом, щоб збільшити межу вимірювання цього амперметра від 2 до 10 А?

Щоб виміряти силу струму, більшу за ту, на яку розрахований амперметр, можна скористатися тим самим амперметром: паралельно амперметру необхідно під’єднати резистор — шунт (рис. 4)

Дано:

R_A=0{,}07 \,\text{Ом}

I_A=2 \,\text{А}

I=10 \,\text{А}

Знайти:

R_{\text{ш}}-?

Розв’язання:

У скільки разів треба збільшити межу:

n=\dfrac{I}{I_A}=\dfrac{10}{2}=5

Опір шунта:

R_{\text{ш}}=\dfrac{R_A}{n-1}

Підставляємо числа:

R_{\text{ш}}=\dfrac{0{,}07}{5-1}=\dfrac{0{,}07}{4}=0{,}0175 \,\text{Ом}

Відповідь: треба під’єднати шунт опором 0,0175 Ом (тобто 17,5 мОм).

10. Складіть задачу за рис. 40.2 і розв’яжіть її.

Задача. Обчисліть загальний опір ділянки кола AD, зображеної на рис. 40.2, якщо опір кожного з резисторів R1 − R6 становить 12 Ом.

Обчисліть загальний опір ділянки кола AD, зображеної на рис. 40.2

Дано:

R_1=R_2=R_3=R_4=R_5=R_6=12 \,\text{Ом}

Знайти:

R_{\text{заг}}-?

Розв’язання:

Між вузлами A і B резистори R1 та R2 паралельно:

R_{AB}=\dfrac{R_1}{2}=\dfrac{12}{2}=6 \,\text{Ом}

Між вузлами C і D резистори R3, R4, R5 паралельно:

R_{CD}=\dfrac{R_3}{3}=\dfrac{12}{3}=4 \,\text{Ом}

Ці дві ділянки послідовно (верхня вітка):

R_{\text{верх}}=R_{AB}+R_{CD}=6+4=10 \,\text{Ом}

R6 паралельно до всієї верхньої вітки:

R_{\text{заг}}=\dfrac{R_{\text{верх}} \cdot R_6}{R_{\text{верх}}+R_6}=\dfrac{10 \cdot 12}{10+12}=\dfrac{120}{22}\approx 5{,}45 \,\text{Ом}

Відповідь: загальний опір ділянки становить приблизно 5,45 Ом.

Паралельне з’єднання провідників - Бар'яхтар

ВПРАВА № 40

Оцініть матеріал

Коментарі

Залишити відповідь: